Risk management - Monte Carlo simulation
Monte Carlo simulation
When you have ‘n’ activities and ‘y’ values in the range then the number of combination of values is ‘y’ to the power of ‘n’.
We can see this in a little more detail.
Let’s say that you have 10 activities that you have assigned a range of values that differ for each one.
The range of values for each activity is 1 to 10.
How many combinations are there?
Well it depends how accurately you wish to control the value.
In the above example we could have the following:
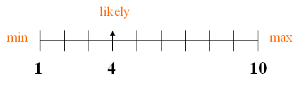
Range:
| LOW: | 1 |
| LIKELY: | 4 (note that the most likely value doesn’t have to be in the middle of the high and low values) |
| HIGH: | 10 |
If we are able to control any value that could occur we might have the following number of possible values:
At + or – 1% there will be 100/2 = 50 potential values (for example a value could lie between 3.6 and 3.8, a difference of 0.2 = 0.2/10 = 2%, that is 50 potential values in range 1 to 10).
or
At + or – 2% there will be 100/4 = 25 potential values.
or
At + or – 5% there will be 100/10 = 10 potential values.
Or
At + or – 10% there will be 100/20 = 5 potential values.
In the above example we are assuming that we can control the value to + or – 5% giving 10 values.
You can see that the more accurate you can control a value the more potential vales there are for a given range.
For a total of 10 activities there will be a total potential combinations of 10 (the number of values within each range) to the power of 10 The number of activities.
Had there been 30 activities the combinations would have been 10 to the power of 30.
That is a lot of combinations.
We clearly don’t have the time to examine what will happen in the project by looking at all the combinations so we have to employ an alternative technique called Monte Carlo Simulation [see Monte Carlo Simulation part 2].