Risk management - Simple network no lag
Simple network no lag
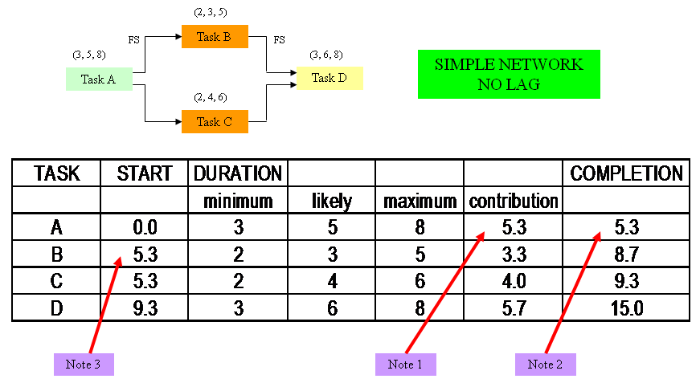
The above diagram represents a spreadsheet for the first of the previous activity networks where Task B and Task C begin at the same time.
The spreadsheet shows the following fields:
TaskLists the task activities as described in the network.
StartThis is the start time of each task as calculated in the spreadsheet.
DurationThese are the 3 point estimates showing the MINIMUM, LIKELY and MAXIMUM.
ContributionThis is the average of the 3 point estimate values (MINIMUM + LIKELY + MAXIMUM)/3.
CompletionThis is the calculated end date or completion for each task. In the main this is the sum of the start value and the contribution, however, this is slightly more complex for activity networks where probabilities are taken into account [see complex branching].
Note 1:
As referred to above this is the sum of the minimum, likely and maximum values and divided by 3 to get the average. In the same manner as for costs it is a way of weighting the 3 point estimate.
Note 2:
The completion date is the sum of the start and the contribution values.
Note 3:
The start is 0.0 for the first task in the network. Task B naturally will start from the end date of Task A. In the case of Task C this will also take its start from the completion of Task A.
Task D can not begin until the end of whatever is the longest task of either B or C. In this case it is Task C. So, the start of Task D is the end of Task C at a value of 9.3. The final activity network completion date will be the end of Task D which is 9.3 + 5.7 (its 3 point estimate contribution) = 15.0.
Simulation
The spreadsheet simulation will carry out perhaps 300 to 1000 iterations and each time will firstly set Task A to a value based upon its 3 point estimate.
This will lead to a completion time for Task A which will be the start time of Tasks B and C. Each of these will in turn have a duration based upon their 3 point estimates affording individual completion dates. Eventually, there will be a value calculated for the completion date of Task D.
This final completion date will be recorded.
Over many iterations a MONTE CARLO distribution will result, having a MINIMUM duration of (3 + 2 + 3) = 8 weeks and a MAXIMUM of (8 + 6 + 8) = 22 weeks.
Note that the MAXIMUM time is based upon the longer of the 3 point estimate times for Task C of 6 weeks.
From this data a graph of PROBABILITY versus TOTAL DURATION will be formed.
In a similar vein to the ‘cost’ scenario we will be able to, for example, set a ‘total duration’ at which there is a ‘likelihood’ of 20% of it being exceeded.
The TOTAL DURATION added on to the start date of 0.0 will give the project COMPLETION DATE.
In addition, CORRELATED EVENTS could be included as for the ‘cost risk assessment’. For this one would need to identify the INDEPENDENT task and then the DEPENDANT tasks which take their lead from it according to the underlying cause.